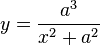Maria Gaetana Agnesi , la "bruja" de las matemáticas

Maria Gaetana Agnesi , nació en Milán el 16 de mayo de 1718 y allí mismo murió en 9 de enero de 1799, se la conoce por haber sido una gran matemática, filósofa y lingüista.

      A los 20 años se centra en estudiar las matemáticas y la religión. Gran influencia que tuvo en ella el monje matemático Ramiro Rampinelli, que había enseñado matemáticas en Roma y en Bolonia, ese ambiente científico-monacal marcó la vida de la matemática italiana.

      En 1748 publicó  "Instituzioni analítiche ad uso della gioventù italiana" en el que trata el cálculo integral y diferencial. Cuando se tradujo al inglés y al francés tuvo una gran importancia ya que reunía y ademas con un buen orden desde el álgebra lineal hasta las ecuaciones diferenciales.

      Entre los años 1750 y 1752 ejerció de catedrática de matemáticas en la Universidad de Bolonia. Durante los cuarenta y siete años siguientes dedico su vida a los pobres hasta su muerte.

      

      La curva llamada indebidamente Bruja de Agnesi  no la descubrió ella , ni lo pretendió, y el nombre de "bruja" seguramente lo aportó el azar de una mala traducción al inglés.


      Para las matemáticas Agnesi ha destacado por su influencia en la distribucion de la enseñanza del cálculo. Es una de las mujeres más citadas en las reflexiones sobre el papel histórico de la mujer en la matemática:  las Instituzioni analítiche son según algunos la obra matemática de autoría femenina más antigua que se conserva.

       En 1748 se publica en Milán  Instituzioni analítiche ad uso della gioventú italiana, la obra más famosa de Agnesi. El primer tomo está dedicado a las magnitudes finitas, y el segundo se ocupa del análisis de infinitesimales.

        La obra gana importancia entre los matemáticos de la época. Las Instituzioni exponen los conocimientos utilizando ejemplos,y una gran armonía entre trabajos de muchos matemáticos que habían estado separados, uniéndolos de una forma clara y concisa. Las 1.000 páginas de texto y las 50 de ilustraciones resultan sin embargo muy familiares al lector moderno, reflejando el mayor mérito de Agnesi: redacta el primer texto completo de Cálculo, desde el álgebra hasta las ecuaciones diferenciales. Superando además intentos anteriores de otros matemáticos, singularmente la de L'Hopital en su libro Analyse des infiniment petits.

        Lo mas destacado son los tratamientos de máximos y mínimos y la integración del cálculo, presentando en la misma obra el diferencial y el integral, y los considera como inversos. Se ha remarcado  la claridad, el orden, la precisión, y el uso afortunado de los ejemplos. Pero tiene también algunos fallos, o por decirlo de otra manera cadencias en las funciones trigonométricas aunque en otras ediciones resolvió esto, pero  no se trataban las series de potencias, entre otras cadencias.

        

        Entre los afortunados ejemplos del libro hay uno, al final del primer volumen, que consiguió para María Gaetana Agnesi un lugar en los índices onomásticos de los libros de texto, y en los manuales de fórmulas y tablas matemáticas, y que la ha hecho famosa en mayor medida que todos sus otros méritos: La bruja de Agnesi.

CURIOSIDAD:

Realmente esta curva no la descubrio ella, se trata de una curva que Fermat había estudiado en 1703, y para la que Grandi, en 1718, había dado un método de construcción.

Lo de "bruja" es un error de traducción; sólo usan ese término el inglés y las lenguas que han copiado el nombre del inglés. Grandi llamó a la curva versoria en latín, y versiera en italiano. Es un término naval, que identifica la cuerda o cabo que hace girar la vela. María Gaetana Agnesi escribió a su vez la versiera, añadiendo el artículo femenino. John Colson, un traductor de Cambridge con poco conocimiento del italiano, llama a la curva witch ('bruja'), debido a que "confundió" versiera con avversiera (que en italiano significa 'diablesa', 'demonia'. La dependencia que el idioma español tenía del idioma inglés acabó por embrujarla también en castellano. En otros idiomas se habla de loci (en latín, 'lugares' geométricos, curvas) de Agnesi.

La curva es asintótica al eje X, a la derecha y a la izquierda, y sólo se representa por tanto en un entorno del origen, en el que alcanza un máximo justo al cruzar el eje Y. Ese entorno montañoso, y la altura del máximo, vienen determinados por un único parámetro a, que es precisamente la altura del punto máximo alcanzado en x = 0, es decir, el punto (0,a) siempre está en la curva y además es su valor máximo.

El método de construcción es sencillo; para obtener un punto cualquiera de la curva:

• Trácese una circunferencicirencia, con centro en el punto (0, a/2)
• Desde el origen, (0, 0), trácense rectas que crucen con la recta y=a (recta OA en la figura, en la que a=10)
• El punto P de la bruja será aquel en que se crucen las rectas BP (horizontal que pasa por el corte entre OA y la circunferencia) y AP (vertical que pasa por el corte entre OA y la recta y=a).

El conjunto de las rectas OA del plano determina el de los puntos de la curva de Agnesi.

Con un poco de geometría (sólo se requieren criterios de igualdad de ángulos, de semejanza de triángulos y el teorema de pitágoras, más muy poca álgebra) se demuestra que la ecuación de la bruja de Agnesi es:

Y las ecuaciones paramétricas son:

Agnesi no presenta ecuaciones paramétricas, pese a que el tratamiento hubiera sido más sencillo, a través de  y