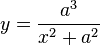Sophie Germain , un cambio sobre los prejuicios de mujeres matemáticas

     Marie-Sophie Germain nació en Paris el 1 de abril de 1776 y murió el 27 de junio de 1831 fue unadestacada matemática francesa cuyas principales contribuciones son la teoría de números y la teoría de la elasticidad. Una de las más importantes fue el estudio de los que posteriormente fueron nombrados como números primos de Sophie Germain (números primos cuyo doble incrementado en una unidad es también un número primo).
 ejemplo: (7+3.5)x2=11
               (11+5.5)x2=33

     Germain estuvo interesada en los conocimientos de Joseph-Louis Lagrange , después del periodo lectivo le envió un trabajo y comenzó a escribirle con el apodo de «Sr. Le Blanc», que era un antiguo estudiante de Lagrange, le envió varios artículos. A Lagrange le gusto tanto que le pidió una entrevista  a Le Blanc y Germain tuvo que decir quien era ella en realidad. Al descubrir este talento matemático que tenia Germain decidió se su mentor. Estudio matematicas y luego fue a Alemania y se casó con un francés.

     En 1804, después de leer a Carl Friedrich Gauss en su famoso Disquisitiones Aritmeticae (1801), inspirada por  este escrito sobre la teoría de los números, Sophie empezó a estudiar sola esta rama de la aritmética superior. Comenzó a cartearse con éste, de nuevo bajo el mismo pseudónimo. Dos años después también Gauss conoció la verdadera identidad.

     Sin embargo, en 1808 cuando Gauss fue nombrado profesor de astronomía en la Universidad de Göttingen, el interés del matemático se derivó hacia las matemáticas aplicadas y ambos dejaron de cartearse ya que  Gauss estaba tan ocupado con su trabajo que solo le contestaba cuando el trabajo se relacionaba con sus propios teoremas.

    Germain en 1811 intenó participar en un concurso de la Academia Francesa de las Ciencias para explicar los fundamentos matemáticos desarrollados por un matemático alemán aplicados al estudio Ernst Chladni sobre las vibraciones de las superficies elásticas. Lo intento deos veces pero fue rechazada pero finalmente en 1816 ganó el concurso y paso a ser una mas de los grandes matemáticos de la historia.

CONTRIBUCIONES MATEMÁTICAS:

Contribuciones

Una de las mayores contribuciones de Germain a la teoría de números fue la demostración de un caso particular del Último Teorema de Fermat: si x, y, z son enteros y x⁵ + y⁵ = z⁵, entonces al menos uno de ellos (x, y, o z) es divisible por cinco.

También se conoce como identidad de Sophie Germain la que expresa para dos números x e y que:

Por último, fueron nombrados como números primos de Sophie Germain a los números primos cuyo doble incrementado en una unidad es también un número primo. Se conjetura que existen infinitos números primos de Sophie Germain, pero éste se trata de otro de los teoremas sin resolver de las matemáticas.

CURIOSIDAD:

     
      1) La pasión de Sophie Germain por las Matemáticas era tal que su padre, para impedirle que estudiase por las noches, le escondía las velas que la iluminaban.
      2) Cuando Germain le pidio a uno de los generales de Napoleón , a quien Germain conocía personalmente, para que resguardara de cualquier daño a Gauss ante la ocupación de  Brunswick ( ciudad natal de Gauss). Pernety  localizó al matemático alemán y le dijo quien era su protectora, él todavía no sabia quien era ella . Entonces Germain le escribió a Gauss una carta en la que admitía su condición femenina y le decia que ella era Le Blanc

Emma Castelnuovo, maestra matemática de vocación

Matemáticas de Ayer y Hoy

"El objetivo principal del curso de geometría intuitiva es el de suscitar, a través de la observación de miles de hechos de la técnica, del arte y de la naturaleza, el interés del alumno por las propiedades fundamentales de las figuras geométricas y con ello el gusto y el entusiasmo por la investigación. Y este gusto no puede nacer, en mi opinión, si no es haciendo participar al alumno en el trabajo creativo. Es necesario, por una parte, animar la natural e institiva curiosidad que tienen los niños de 11 a 14 años conduciéndoles al descubrimiento de las verdades matemáticas, tratando de darles la impresión de haberlo hecho por sí mismos, y por otra parte, hacerles sentir progresivamente la necesidad de un razonamiento lógico."


Es este uno de los fragmentos de la obra "Geometría Intiutiva" de la famosa Emma Castelnuovo, profesora italiana en los años sesenta. Emma estudió en el Instituto Matemático de la Universidad de Roma, donde obtuvo la licenciatura en Matemáticas en el año 1936 con un trabajo sobre Geometría Algebraica.

Al terminar sus estudios universitarios trabajó como bibliotecaria en el mismo Instituto Matemático de Roma durante los años 1936, 1937 y 1938. Este instituto lleva el nombre de "Guido Castelnuovo" en honor a su padre, gran geómetra italiano. En 1938 se presentó a las oposiciones para ingresar como profesora en una Escuela de Enseñanza Secundaria. No le dieron la cátedra debido a las leyes raciales vigentes durante el periodo de fascismo italiano y por la misma razón perdió su trabajo como bibliotecaria. Desde 1939 a 1943 trabajó como profesora en la Escuela Israelita de Roma organizada en ese período. La liberación de Roma en junio de 1944 le permitió presentarse y obtener la cátedra en una Escuela Estatal de Enseñanza Secundaria de primer ciclo (alumnos de 11 a 14 años). Ese mismo año organizó un ciclo de conferencias sobre la enseñanza de las Matemáticas.

En 1946 dio una conferencia y escribió un artículo sobre “El Método Intuitivo” para enseñar Geometría en el Primer Ciclo de Secundaria. Las ideas que expone en este artículo son las que le llevaron a escribir y publicar, en el año 1949, su primer libro titulado “Geometría Intuitiva” desarrollando en él unas ideas y unos métodos que nada tenían que ver con los programas oficiales vigentes.

En 1950 nace la C.I.E.A.E.M. (Comisión Internacional para el Estudio y Mejora de la Enseñanza de las Matemáticas) y es nombrada miembro de dicha Comisión en 1951. Con este motivo conoce y trabaja con Piaget, Gattegno, Puig Adam y otros. La C.I.E.A.E.M. promueve en 1958 la publicación de un libro titulado "El material para la enseñanza de las Matemáticas" con artículos de personas muy relevantes en didáctica de la matemática, entre ellos Emma Castelnuovo y Puig Adam. En 1963 se publica su libro "Didattica della Matematica" y a partir de ese año da muchos cursos y conferencias tanto en Italia como en otros países y participa en casi todos los congresos y comisiones nacionales e internacionales sobre educación matemática.

Por otra parte, organiza en Roma dos exposiciones con trabajos de sus alumnos en los años 1971 y 1974. Estas exposiciones, que son un planteamiento vivo de sus planteamientos didácticos, dan lugar a la publicación de dos libros titulados "Documenti di un'esposizione di matematica" en 1972 y "Matematica nella realtá" en 1976. Desde 1977 a 1982 acude a Niger en cuatro ocasiones y participa en experiencias didácticas en clases con alumnos nigerianos de escuelas secundarias.

En dos de estas ocasiones es la UNESCO quien organiza estas actividades. En 1984 colabora en libros de Matemáticas para el segundo ciclo de la enseñanza secundaria italiana (alumnos de 14 a 18 años). En enero de 1993 publica un libro de divulgación matemática que lleva el título de Pentole, ombre e formiche. Es de destacar que Emma Castelnuovo, por decisión personal, ha enseñado siempre en la Escuela Secundaria de primer ciclo (Escuela Media), para alumnos de 11 a 14 años.


CURIOSIDADES:

Ha estado en España en varias ocasiones, su participación en las II Jornadas Regionales de Didáctica de la Matemática que tuvieron lugar en Zamora en 1987 y en las que coordinó una mesa de trabajo sobre Geometría. En los II Encuentros Extremeños de Profesores de Matemáticas dio una conferencia sobre "Los Fractales"* y habló sobre los programas de Matemáticas del pasado y del futuro.

*Es complicado dar una definición general de fractales porque muchas de estas definiciones no se pueden aplicar a todas las familias de fractales existentes. Sin embargo, todos los fractales tienen algo en común, ya que todos ellos son el producto de la iteración, repetición, de un proceso geométrico elemental que da lugar a una estructura final de una complicación aparente extraordinaria. Es decir que cada porción del objeto tiene la información necesaria para reproducirlo todo, y la dimensión fractal no necesariamente entera.

Emmy Noether, la madre del álgebra moderna

 El 23 de marzo de 1882 nació en Erlangen, Emmy Amalie Noether. Su padre, Max Noether, era profesor de matemáticas en la universidad de Erlangen y era conocido por sus investigaciones sobre funciones algebraicas.

Después de una formación básica estudió francés e inglés, para ser profesora de idiomas. Al estar su padre metido en el mundo de las matemáticas ella se vio influida. La Universidad de Erlangen prohibía la admisión de mujeres estudiantes pero se les autorizaba a ir a clase con un permiso especial aunque sin derecho a examinarse.  

En 1904 en Erlangen cambian los estatutos de la Universidad, y pudo proseguir sus estudios de doctorado sobre la teoría de invariantes bajo la influencia de Paul Gordan. En 1907 obtuvo el grado de doctora “cum laude” con la memoria titulada: “Sobre los sistemas completos de invariantes para las formas bicuadráticas ternarias”, publicada en 1908. 

En la Universidad de Erlangen trabajaba en ayudar a su padre pero sin cobrar. Durante estos dos años tuvo dos tutores (Emst Fischer y Bernhard Schmidt) que despertaron su interés por el álgebra abstracta. En 1915 fue invitadaa trabajar con David Hilbert y Félix Klein en  la Universidad de Göttingen. Pese a toda una serie de importantísimos trabajos sobre invariantes diferenciales el reglamento de la Universidad indicaba que los candidatos debían ser hombres, y no pudo presentarse a oposiciones como profesara universitaria. Hilbert y Noether idearon una forma para que ella pudiera dar clases: las clases se anunciaban bajo el nombre de Hilbert y ella figuraba como ayudante. Emmy escribió sus ideas sobre conservación de la energía, que dio lugar a  los famosos resultados conocidos por los físicos como los Teoremas de Noether, publicados en 1918. Finalizada la Primera Guerra Mundial por primera vez las mujeres tuvieron derecho a voto y fue derogado el anterior reglamento de oposiciones. En 1919 Emmy presentó como “tesis de habilitación” su trabajo "Invariante Variationsprobleme" junto con doce artículos ya publicados y dos manuscritos adicionales, que tuvieron una gran influencia en el Álgebra Abstracta. En 1922 fue nombrada “profesora extraordinaria y no oficial”. No cobraba, pero pudo obtener pequeñas retribuciones, por su grado de experta en álgebra. El periodo de Göttingen sólo fue interrumpido por dos breves estancias como profesor invitado en Moscú (1928/29) y en Frankfurt Am Main (1930). En septiembre de 1932 fue invitada al Congreso Internacional de Matemáticos de Zurich y ese mismo año recibió con Artin, el Alfred Ackermann-Teubner Memorial, premio al Avance del Conocimiento Matemático. 

A pesar del reconocimiento la llegada de Hitler al poder le obligaron a reorientar su carrera. Al ser judía y liberal le obligó a abandonar Alemania. En abril de 1933 se exilió. Se marchó a los Estados Unidos como profesora invitada durante un año a una universidad femenina, el Bryn Mawr College (Pennsylvania). En febrero de 1934 comenzó a trabajar en Princeton, New Jersey, en el Instituto de Estudios Avanzados, donde también se encontraba Albert Einstein. En verano volvió por última vez a Alemania para ver a su hermano Fritz, visitar viejos amigos y cerrar su casa. Murió el 14 de abril de 1935 como consecuencia de una operación. Tenía 53 años y estaba en el apogeo de su fuerza creadora. 

TEOREMA DE NOETHER

En física cuántica la descripción de un sistema se realiza mediante el lagrangiano cuántico que es un funcional definido sobre el espacio de Hilbert relevante para el sistema. Cuando dicho lagrangiano es invariante respecto a un grupo uniparamétrico de aplicaciones unitarias de dicho espacio de Hilbert, entonces cada uno de los generadores del álgebra de Lie de dicho grupo es un observable que es una constante del movimiento en el sentido de que:




Podemos exponer una transformación que sea mezcla de diferentes campos:




donde es un parámetro infinitesimal y los están fijados.

Si es invariante bajo la transformación, entonces donde




Todo esto significa que la carga del sistema se conservará:




La naturaleza física de la corriente y de la carga vendrá dada por una forma específica de la transformación.

Sofía Kovalevskaya, autodidacta en la ciencia matemática

Una mujer extraordinaria, Sofía Kovalevskaya, no solo fue una gran matemática, sino también escritora y defensora de los derechos de la mujer durante el siglo XIX. Su lucha fue obtener la mejor educación posible en universidades donde comenzaban a abrirles las puertas a las mujeres. Además, su impresionante labor matemática logró modificar la visión arcaica de que las mujeres eran inferiores en las arenas científicas.

Sofía Kovalevskaya nació en 1850 en Palobino, en el seno de una familia rusa. Tomó contacto con las matemáticas a muy temprana edad. Ella declaraba haber estudiado las viejas notas de cálculo de su padre, pero atribuye a su tío Peter el haberle despertado su curiosidad por la matemática. A los 14 años, aprendió trigonometría por sus propios medios para poder entender una sección de óptica de un libro de física que estaba leyendo. El profesor Tyrtov, autor de este libro y también su vecino, quedó muy impresionado con las habilidades de Sofía, y convenció a su padre para que la enviara a San Petersburgo para completar su educación formalmente.

Después de terminar la escuela secundaria, decidió seguir sus estudios a nivel universitario. Pero la universidad más cercana que admitía mujeres estaba en Suiza, y en aquellos tiempos, no era bien visto que una mujer soltera y joven viajara sola.
Para solucionar su problema, Sofía se casó por conveniencia con Vladimir Kovalevsky en Septiembre de 1868.

Dos años después, decidió que continuaría sus estudios bajo la supervisión de Karl Weierstrass en la Universidad de Berlín. Weierstrass era considerado como uno de los más renombrados matemáticos de su tiempo y al principio no tomó muy en serio a Sofía. Sólo después de evaluar una selección de problemas que le había dado, se dio cuenta del genio que tenía entre sus manos. Él, inmediatamente, se hizo cargo personalmente de sus estudios, porque en ese momento la universidad no admitía mujeres.

Sofía estudió con Weierstrass durante cuatro años. Ella misma dijo: “estos años tuvieron la más profunda influencia en mi carrera matemática. Determinaron irrevocable y definitivamente la dirección que seguiría mi labor científica: todo mi trabajo ha sido hecho precisamente en el espíritu de Weierstrass.” Al final de estos cuatro años, ella había escrito tres trabajos científicos originales con la esperanza de obtener su título. El primero de estos artículos ,“On the theory of partial differential equations”, fue publicado en la revista de Crelle, que era considerado un honor para un matemático desconocido. En julio de 1874, Sofía Kovalevskaya obtuvo su doctorado de la Universidad de Gottingen.

En 1880, presentó su artículo sobre integrales abelianas en una conferencia científica y fue muy bien recibida. Nuevamente se enfrentó con el dilema de conseguir empleo en lo que más le gustaba hacer en la vida: matemática. Además, obtuvo una serie de grandes logros: una posición permanente en la universidad, fue invitada a ser editora de una revista matemática, publicó su primer artículo en cristales y en 1885 fue designada directora del departamento de Mecánica. Finalmente, el 10 de Febrero de 1891, murió.

En 1888, presentó el artículo “On the rotation of a solid body about a fixed point” en una competencia para el Prix Bordin de la Academia Francesa de Ciencias y ganó. Antes de este trabajo, sólo se había estudiado el movimiento de un cuerpo rígido alrededor de un punto fijo para dos casos en los que el cuerpo era simétrico. En su artículo, Sofía desarrolló la teoría para un cuerpo no simétrico cuyo centro de masa no se encuentra sobre el eje del mismo.


APORTACIONES CIENTÍFICAS:

Durante su carrera publicó diez artículos en matemática y física matemática. Muchos de estos trabajos fueron teorías pioneras o el ímpetu para futuros descubrimientos. No hay discusión de que Sofía Kovalevskaya fue una persona increíble. El presidente de la Academia de ciencias francesa que le dio el premio Prix Bordin, dijo: “Nuestros miembros han encontrado que su trabajo no es solo testimonio de un conocimiento profundo y amplio, sino también de una gran mente creativa”.

Sus principales aportaciones al campo de las matemáticas fueron:

1. El teorema que lleva hoy el nombre de Cauchy-Kovalevsky*, básico en la teoría de las
ecuaciones diferenciales parciales.
2. Examinó el concepto analítico desarrollado en la obra de Legendre, Abel, Jacobi y
Weiestrass, que dio pie al trabajo de su segundo doctorado.
3. En su trabajo ganador del Premio Bordin, generalizó los resultados de Euler, Poisson y Lagrande que consideraban dos casos elementales de la rotación de un cuerpo rígido alrededor de un punto fijo.
4. Sus estudios sobre la dinámica de los anillos de Saturno.

*Uno de los resultados generales de la teoría de Ecuaciones en Derivadas Parciales (EDP), que se aplica tanto a los casos lineales como no lineales, es el teorema de Cauchy – Kovalevskaya. Aunque resulta un poco complejo, el teorema básicamente afirma que para que una EDP que es analítica en la función incógnita y sus derivadas tiene una única solución analítica. Aunque este resultado que parece establecer la existencia y unicidad de las soluciones, existen ejemplos de EDP de primer orden cuyos coeficientes tienen derivadas de cualquier orden (aunque sin ser analíticas) pero que no tienen solución. Incluso si la solución de una EDP existe y es única, esta puede tener propiedades indeseables.


CURIOSIDADES:

1) El día "Sonia Kovalevsky" sobre Matemáticas, en los High School de Estados Unidos es un programa de la Asociación de Mujeres en Matemáticas (AWM), que promueve la financiación de talleres en los Estados Unidos para alentar a las niñas a explorar las matemáticas.

2) La Fundación Alexander von Humboldt de Alemania otorga un premio bi-anual llamado Sofia Kovalevskaya a prometedores jóvenes investigadores de todos los campos.

Ada Lovelace, la primera programadora de la historia

   Ada Lovelace vivió durante la primera mitad del siglo XIX, bajo bajo la influencia de las ideas clásicas de la sociedad victoriana pero marcado al tiempo del ideal romántico.

Ada Augusta Byron King nació el 10 de diciembre de 1815en  Londres y murió el 27 de noviembre de 1852 en el mismo lugar donde nació, Londres

Ada describió la máquina analítica de Charles Babbage, actualmente es considerada como la primera programadora, desde que escribió la manipulación de los símbolos, de acuerdo a las normas para una máquina de Charles Babbage que aún no había sido construida.Dedujo y previó la capacidad de los ordenadores para ir más allá de los simples cálculos de números, mientras que otros, incluido el propio Babbage, se centraron únicamente en estas capacidades.

Su actitud tan abierta hacia la formación científica hizo que las mujeres de buena posición social pudieran estudiar aunque seguia habiendo desigualdades muy notables entre los hombres y las mujeres.

La vida de Ada está marcada por dos factores: la personalidad estricta de su madre y el ambiente culto y refinado al que pertenecía. Ada vivió condicionada por los dictados de su madre.

Ada fue educada en matemáticas por los mejores tutores conocidos de Londres.

Con 17 años conoció a Charles Babbage, y tanto ella como su madre quedaron impresionadas por su Máquina de diferencias finitas, que deseaba generalizar en una máquina analítica o computadora general.

Se caso con el Honorable William King. el sucesivo nacimiento de sus tres hijos impidió a Ada seguir con sus estudios. A los tres meses de tener a su tercer hijo decidió restablecer el contacto con Babbage, rogándole que le proporcionara un profesor con quien aprender matemáticas. Poco después enfermó y, siguiendo la práctica médica habitual, se le realizaron sangrías y se le suministró morfina y opio. No llegó a reponerse y se le detectó un cáncer en estado avanzado que le producía tremendos dolores.

Ada murió a la edad de 36 años. Babbage continuó intentado la construcción de su máquina analítica pero desistió del proyecto tras numerosos fallos. Ambos fueron olvidados casi completamente hasta que los ordenadores fueron reinventados durante la segunda guerra mundial.

Grace Murray Hopper, la programadora del Ejército

La historia de esta mujer matemática se acerca enormemente a nuestros días, con su muerte hace solo unos 20 años. Hablamos de la mismísima Grace Murray Hopper, nacida en Nueva York en 1906. Desde muy pequeña demostró una gran aptitud para las ciencias y las matemáticas y se tiene constancia de que en el colegio ya destacaba como alumna en matemáticas. Es por esto que miembros de su familia, tales como su abuelo o su padre siempre la animaron a que las estudiara. También le atrajo mucho cualquier tipo de dispositivo mecánico, y así lo demuestra cuando con 7 años desarmó todos los relojes de su casa para ver si podía así entender su funcionamiento.

Su formación académica fue intensa y espectacular, ya que contó con muchas de las escuelas mejor reconocidas del mundo. Hopper estudió en varias escuelas privadas para mujeres y en 1924 ingresó en Vassar College en Nueva York, donde cursó estudios en matemáticas y física, graduándose con honores en 1928. Además obtuvo una beca para cursar un máster en matemáticas en la Universidad de Yale, donde se graduó en 1930. Debido a su gran potencial, Grace recibió la oferta de un puesto como asistente en el departamento de matemáticas de Vassar College, donde permaneció hasta 1943 mientras continuaba sus estudios en Yale, obteniendo el doctorado en matemáticas en 1934.

Al terminar sus estudios, decidió unirse a las fuerzas armadas en 1943 en plena Segunda Guerra Mundial, para lo cual tuvo que obtener un permiso especial. Asistió a la Escuela de cadetes navales para Mujeres, graduándose la primera de su clase en 1944 y obteniendo el rango de teniente. Tras el final de la Segunda Guerra Mundial, Hooper quiso seguir en la Armada pero como ya había cumplido los 40 años en 1946 (el límite eran 38) fue rechazada permaneciendo en la reserva hasta 1966, cuando tuvo que retirarse con el grado de Comandante, por haber alcanzado el límite de edad nuevamente. Pero este retiro duró poco ya que la Armada la volvió a llamar en 1967 para que estandarizara los lenguajes de alto nivel que usaban. Se reincorporó y permaneció en el servicio durante 19 años más. En 1986, Hopper se retiró de la Armada de manera definitiva, siendo en ese momento la oficial de más edad de la Armada de los EE.UU.




APORTACIONES CIENTÍFICAS:

Hopper se especializó en matemáticas y está considerada pionera en el mundo de la informática.

Paralelamente a su trayectoria en la Armada, hizo numerables aportaciones en el ámbito informático. Fue enviada a Harvard para trabajar en el Proyecto de Computación que dirigía el comandante Howard Aiken, la construcción de la Mark I. Además, desarrolló varias aplicaciones contables para la Mark I, que estaba siendo utilizada por una compañía de seguros.



Por otro lado, Hopper empezó a trabajar en la Eckert - Mauchly Corporation en Filadelfia, que en esos momentos estaban desarrollando las computadoras BINAC y UNIVAC I. Trabajó en esa compañía y en sus sucesoras hasta su retiro en 1971. Allí fue donde Hopper realizó sus mayores contribuciones a la programación moderna. En 1952, desarrolló el primer compilador de la historia, llamado A-0, y en 1957 realizó el primer compilador para procesamiento de datos que usaba comandos en inglés, el B-0 (FLOW-MATIC), cuya aplicación principal era el cálculo de nóminas. Tras su experiencia con FLOW-MATIC, Hopper pensó que podía crearse un lenguaje de programación que usara comandos en inglés y que sirviera para aplicaciones de negocios. La semilla de COBOL había sido sembrada, y 2 años después se creó el comité que diseño el famoso lenguaje. Aunque Hopper no tuvo un papel preponderante en el desarrollo del lenguaje, fue miembro del comité original para crearlo, y el FLOW-MATIC fue una influencia tan importante en el diseño de COBOL, que se considera a Hopper como su creadora.

Tras su retiro, se incorporó como asesora en Digital Equipment Corporation, participando en foros industriales, dando unas 200 conferencias por año y participando en programas educativos hasta 1990, cuando la "increíble Grace", que era como la conocían sus amistades, se retiró definitivamente.


RECONOCIMIENTOS:

A lo largo de su vida, recibió numerosos reconocimientos, que incluyen más de 40 doctorados honoris causa, la Medalla Wilbur Lucius Cross de Yale, el rango de capitán en 1973, el de comodoro en 1983 y el de contraalmirante en 1985. Única mujer con el grado de almirante de su país. Podemos destacar:

* En 1950, Grace Hopper recibe el título de « programadora senior », una de las 10 primeras personas que pueden gozar de este título. En una conferencia que llegó a ser célebre, Grace Hopper predijo que el software acabaría por costar más caro que el material (hardware), lo que, en esa época, era difícilmente imaginable.

* En 1969, fue la primera que recibió el premio del « Informático m/f del año ». En 1971, una nueva recompensa anual dedicada a los jóvenes científicos en informática m/f fue creada a su nombre ».

* En 1983, fue promovida a comandante en la "Casa Blanca", dos años más tarde, se la nombró "Almirante Grace Hopper".

* En 1991, un año antes de su muerte, Grace Hopper recibió la "National Medal of Technology" por los éxitos de sus trabajos pioneros en el desarrollo de lenguajes de programación para ordenador que simplifican la tecnología informática y abren la puerta a un universo de utilizadores significativamente más amplio.


CURIOSIDADES:

- A lo largo de gran parte de su carrera, Hopper era muy demandada como oradora en eventos relacionados con la informática. Era conocida por su animado e irreverente estilo de oratoria, así como por sus historias de guerra.

- A menudo, se le atribuye erróneamente la invención del término bug para referirse a un error o fallo en un programa. Trabajando con un Mark II en la universidad de Harvard el 9 de septiembre de 1947, los ingenieros encontraron una mariposilla enganchada a uno de los relés del ordenador y que impedía el funcionamiento del mismo. Dicho lepidóptero pasó a la historia de la informática por ser pegado al libro de registro de actividad del ordenador con el comentario «First actual case of bug being found», en español «Primer caso real de bug encontrado» (el termino bug no se traduce al castellano por considerarse una palabra técnica). Como ella misma reconoció, no fue ella la que encontró el insecto.

Mary Somerville, la reina de la ciencia

                                    

 

Mary Somerville, matemática y científica escocesa,estuvo entregada a las matemáticas y al conocimiento de los avances científicos.

Cuando nace Mary Somerville, Inglaterra presenta un decaimiento del desarrollo científico.
La ciencia en la época de Mary se estaba volviendo compleja y difícil de comprender para los intelectos sin formación, y la investigación experimental requería aparatos costosos, así como más clara implicación en el desarrollo industrial.

Ella inició un aprendizaje autodidacta y en 1804 se casó con Samuel Greig, oficial de marina. Nacieron dos hijos y su marido murió al tercer año de matrimonio.

Su primer “éxito” fue ganar una medalla de plata por la solución de un problema sobre las ecuaciones diofánticas en el Mathematical Repository de Wallace.

En Edimburgo participaba en coloquios y reuniones que se celebraban con frecuencia, y en las que tomó contacto con importantes científicos, entre ellos William Wallace quien orientó sus lecturas matemáticas haciéndole llegar los trabajos de los más importantes matemáticos franceses de la época.

Su segundo matrimonio, en 1812, con su primo William Somerville, inspector médico de la Royal Navy y ademas su marido le apoyaba en sus proyectos.

curiosidad:
Se instalaron en Londres y William, su marido, se hizo socio de la Royal Society, ya que en dicha Institución no se admitían mujeres ni les estaba permitido el acceso a las instalaciones. En su biblioteca él copiaba a mano los artículos que a su mujer le resultaban interesantes para sus investigaciones.

Visita París, en 1817, para encontrarse con los más importantes matemáticos de la época como Lagrange, Poisson y Laplace, quienes les mostraron el avance de sus trabajos. Para una científica como ella, el estudio de estos materiales era fundamental dado que en Inglaterra le resultaba muy difícil conseguir tratados matemáticos de esta importancia.

En 1826 Mary Somerville escribió su primer artículo.

En 1827, Lord Brougham, a requerimiento de la Royal Society; instó, a Mary, a través de su marido, a que realizara una versión traducida al inglés de laMécanique Céleste de Laplace. La primera idea era hacer una versión sencilla para una colección que se preocupaba de la divulgación de las ideas científicas para no expertos, pero el trabajo resultó tan interesante que los editores, a instancias de John Herschel, decidieron publicarlo como tratado de importancia fundamental. El preámbulo, A Preliminary Dissertation era un compendio de desarrollos matemáticos e ideas fundamentales de física imprescindibles para comprender la obra de Laplace.

Su libro The Connection of the Physichal Sciences, publicado en 1834 fue un éxito. Uno de los mayores logros fue contar con la colaboración de científicos tan importantes como Faraday, Wollaston, Herschel, Maxwell y Whewell. En él, Mary Somerville presentaba una visión del mundo físico que contenía una explicación matemática compleja, pero evitando, en la medida de lo posible, el uso excesivo de fórmulas o símbolos matemáticos.

Su dedicación a la astronomía le llevó a realizar cálculos relativos a un posible planeta que perturbaba la órbita de Urano. Estos datos posibilitaron la localización de Neptuno por John Adams.

En 1835 recibió, junto a Carolina Herschel, la medalla de honor de la Sociedad de Astronomía.

En 1848 publica Physical Geography y en 1865, a los 85 años de edad, publica Molecular and Microscopic Science, una aproximación a la composición de la materia, el concepto de calor y las partículas microscópicas. Incluía diagramas de los experimentos de Ernnest Chladni con placas vibratorias, fenómeno del que también se había ocupado Sophie Germain.

En 1870, a los 90 años recibió la medalla de oro de la Real Sociedad Geográfica Victoriana. sus hijas, que le ayudaron a escribir sus memorias que tituló Personal Recollections. Y finalmente en 1872, a los 92 años la muerte le sorprendió en Italia.

Hipatia de Alejandría, "la filósofa"

¿Qué sabemos hoy en día de la gran Hipatia? Pues la verdad es que no sabemos tanto como quisiéramos, puesto que no se han conservado obras suyas. Todo lo que podemos conocer de ella nos llega a través del testimonio de terceros. Es por esto que hay que tener cuidado con las fuentes que se consultan, ya que sus contemporáneos la describen con cierta subjetividad (ante todo somos seres humanos, y nuestro punto de vista siempre se verá reflejado en nuestros escritos). Tenemos, entre otros, el testimonio de Sócrates Escolástico, coetáneo de Hipatia, que nos narra los hechos desde una perspectiva digamos que moderada, ya que, a pesar de ser cristiano, reconoce la dignidad del personaje de Hipatia y rechaza la indignidad de su asesinato a manos de fanáticos. En el otro extremo tenemos el testimonio de Juan, Obispo de Nikiu, que 2 siglos más tarde se alinea claramente a favor de los asesinos de Hipatia, condenando sus "estratagemas satánicas" y su "magia". Tras un largo estudio, se puede sintetizar la biografía de la filósofa y matemática como pueden leer a continuación.

Hipatia de Alejandría nació alrededor de 370 en Alejandría, en el antiguo Egipto. Era hija del matemático y filósofo Teón de Alejandría y es casi seguro que estudió matemáticas bajo la guía e instrucción de su padre. Gracias a su esfuerzo y dedicación, Hipatia llegó a ser directora de la escuela Neoplatónica de Alejandría hacia el 400 d.C. Allí impartía clases de matemáticas y filosofía, enseñando particularmente la filosofía neoplatónica. Hipatia basaba sus enseñanzas en las de Plotino, el fundador del Neoplatonismo, y de Iámblico, uno de los desarrolladores del Neoplatonismo alrededor del 300 d.C. Profundizó en estas ideas filosóficas con un énfasis científico mayor que los seguidores anteriores del Neoplatonismo. Todos los comentaristas la describen como una maestra carismática.


Hipatia llegó a simbolizar aprendizaje y ciencia, lo que los primeros cristianos identificaban con paganismo. Sin embargo, entre los alumnos a los que enseñó en Alejandría había muchos cristianos importantes. Uno de los más famosos es Sinesio de Cirerne, quien después sería obispo de Temópolis. Se conservan muchas de las cartas que Sinesio escribió a Hipatia y vemos a alguien que estaba lleno de admiración y respeto por las habilidades científicas y de aprendizaje de Hipatia.


APORTACIONES CIENTÍFICAS:

Hipatia se dedicó, durante veinte años, a investigar y enseñar Matemáticas, Geometría, Astronomía, Lógica, Filosofía y Mecánica en el Museo, ocupaba la cátedra de Filosofía platónica por lo que sus amigos y compañeros la llamaban "la filósofa".

Su trabajo más extenso fue en álgebra. Escribió un comentario sobre la Aritmética de Diofanto (considerado como el padre del álgebra) en el que incluía soluciones alternativas y nuevos problemas. También escribió, en ocho libros, un tratado sobre la Geometría de las Cónicas de Apolonio (a quien se deben los epiciclos y deferentes para explicar las órbitas irregulares de los planetas). Colaboró con su padre en la revisión, mejora y edición de los Elementos de la Geometría de Euclides, cuya edición es la que aún se emplea en nuestros días, escribiendo un tratado sobre el mismo.

Escribió un Canon de Astronomía, dedicándose además a realizar la revisión de las Tablas Astronómicas de Claudio Tolomeo, conocidas por su inclusión en el Canon Astronómico de Hesiquio. También cartografió diversos cuerpos celestes, confeccionando un planisferio.

Además de la filosofía, matemáticas y astronomía, se interesó por la mecánica y las tecnologías prácticas. En las Cartas de Sinesio están incluidos sus diseños para varios instrumentos, incluyendo un astrolabio plano, que nos sirve para medir la posición de las estrellas, los planetas y el Sol. También desarrolló un aparato para la destilación del agua, así como un hidroscopio para medir la presencia y el nivel del agua, y un hidrómetro graduado de latón para determinar el peso específico de los líquidos. Por último, se la supone inventora del aerómetro, instrumento que se usa para medir las propiedades físicas del aire u otros gases.


CURIOSIDADES:

1) El asteroide (238) Hypatia descubierto en 1884 y el cráter lunar Hipatia fueron bautizados en su honor. Este último se sitúa junto a los cráteres que recuerdan a su padre, Teón, y a los patriarcas Cirilo y Teófilo. Con unas medidas de 28 x 41 km, se localiza en los 4,3°S y 22,6°E del meridiano lunar. Unos 70 km al norte del cráter se halla un sistema de canales de 180 km de longitud llamado Rimae Hypatia, un grado al sur del ecuador lunar, a lo largo del Mare Tranquillitatis.





2) Algunos científicos españoles, entre los que se encuentran diversos astrónomos, pedagogos, antropólogos y sociólogos, han criticado el protagonismo de Hipatia de Alejandría en la película 'Ágora', dirigida por el director español Alejandro Amenábar. Esto se debe a que aunque en la película sí se refleja el papel de Hipatia como una de las primeras mujeres dedicada a la astronomía y a las matemáticas, a juicio de los científicos, se deja entrever que ella fue la descubridora de la teoría heliocéntrica y no fue así, ya que no fue hasta Kepler cuando se descubrió.




DIVERSAS VERSIONES:

El asesinato de Hipatia en marzo del año 415 en Alejandría dio lugar a una gran polémica. El siguiente vídeo, además de recoger la información facilitada anteriormente, nos explica algunos de los distintos motivos de su muerte.

Maria Gaetana Agnesi , la "bruja" de las matemáticas

Maria Gaetana Agnesi , nació en Milán el 16 de mayo de 1718 y allí mismo murió en 9 de enero de 1799, se la conoce por haber sido una gran matemática, filósofa y lingüista.

      A los 20 años se centra en estudiar las matemáticas y la religión. Gran influencia que tuvo en ella el monje matemático Ramiro Rampinelli, que había enseñado matemáticas en Roma y en Bolonia, ese ambiente científico-monacal marcó la vida de la matemática italiana.

      En 1748 publicó  "Instituzioni analítiche ad uso della gioventù italiana" en el que trata el cálculo integral y diferencial. Cuando se tradujo al inglés y al francés tuvo una gran importancia ya que reunía y ademas con un buen orden desde el álgebra lineal hasta las ecuaciones diferenciales.

      Entre los años 1750 y 1752 ejerció de catedrática de matemáticas en la Universidad de Bolonia. Durante los cuarenta y siete años siguientes dedico su vida a los pobres hasta su muerte.

      

      La curva llamada indebidamente Bruja de Agnesi  no la descubrió ella , ni lo pretendió, y el nombre de "bruja" seguramente lo aportó el azar de una mala traducción al inglés.


      Para las matemáticas Agnesi ha destacado por su influencia en la distribucion de la enseñanza del cálculo. Es una de las mujeres más citadas en las reflexiones sobre el papel histórico de la mujer en la matemática:  las Instituzioni analítiche son según algunos la obra matemática de autoría femenina más antigua que se conserva.

       En 1748 se publica en Milán  Instituzioni analítiche ad uso della gioventú italiana, la obra más famosa de Agnesi. El primer tomo está dedicado a las magnitudes finitas, y el segundo se ocupa del análisis de infinitesimales.

        La obra gana importancia entre los matemáticos de la época. Las Instituzioni exponen los conocimientos utilizando ejemplos,y una gran armonía entre trabajos de muchos matemáticos que habían estado separados, uniéndolos de una forma clara y concisa. Las 1.000 páginas de texto y las 50 de ilustraciones resultan sin embargo muy familiares al lector moderno, reflejando el mayor mérito de Agnesi: redacta el primer texto completo de Cálculo, desde el álgebra hasta las ecuaciones diferenciales. Superando además intentos anteriores de otros matemáticos, singularmente la de L'Hopital en su libro Analyse des infiniment petits.

        Lo mas destacado son los tratamientos de máximos y mínimos y la integración del cálculo, presentando en la misma obra el diferencial y el integral, y los considera como inversos. Se ha remarcado  la claridad, el orden, la precisión, y el uso afortunado de los ejemplos. Pero tiene también algunos fallos, o por decirlo de otra manera cadencias en las funciones trigonométricas aunque en otras ediciones resolvió esto, pero  no se trataban las series de potencias, entre otras cadencias.

        

        Entre los afortunados ejemplos del libro hay uno, al final del primer volumen, que consiguió para María Gaetana Agnesi un lugar en los índices onomásticos de los libros de texto, y en los manuales de fórmulas y tablas matemáticas, y que la ha hecho famosa en mayor medida que todos sus otros méritos: La bruja de Agnesi.

CURIOSIDAD:

Realmente esta curva no la descubrio ella, se trata de una curva que Fermat había estudiado en 1703, y para la que Grandi, en 1718, había dado un método de construcción.

Lo de "bruja" es un error de traducción; sólo usan ese término el inglés y las lenguas que han copiado el nombre del inglés. Grandi llamó a la curva versoria en latín, y versiera en italiano. Es un término naval, que identifica la cuerda o cabo que hace girar la vela. María Gaetana Agnesi escribió a su vez la versiera, añadiendo el artículo femenino. John Colson, un traductor de Cambridge con poco conocimiento del italiano, llama a la curva witch ('bruja'), debido a que "confundió" versiera con avversiera (que en italiano significa 'diablesa', 'demonia'. La dependencia que el idioma español tenía del idioma inglés acabó por embrujarla también en castellano. En otros idiomas se habla de loci (en latín, 'lugares' geométricos, curvas) de Agnesi.

La curva es asintótica al eje X, a la derecha y a la izquierda, y sólo se representa por tanto en un entorno del origen, en el que alcanza un máximo justo al cruzar el eje Y. Ese entorno montañoso, y la altura del máximo, vienen determinados por un único parámetro a, que es precisamente la altura del punto máximo alcanzado en x = 0, es decir, el punto (0,a) siempre está en la curva y además es su valor máximo.

El método de construcción es sencillo; para obtener un punto cualquiera de la curva:

• Trácese una circunferencicirencia, con centro en el punto (0, a/2)
• Desde el origen, (0, 0), trácense rectas que crucen con la recta y=a (recta OA en la figura, en la que a=10)
• El punto P de la bruja será aquel en que se crucen las rectas BP (horizontal que pasa por el corte entre OA y la circunferencia) y AP (vertical que pasa por el corte entre OA y la recta y=a).

El conjunto de las rectas OA del plano determina el de los puntos de la curva de Agnesi.

Con un poco de geometría (sólo se requieren criterios de igualdad de ángulos, de semejanza de triángulos y el teorema de pitágoras, más muy poca álgebra) se demuestra que la ecuación de la bruja de Agnesi es:

Y las ecuaciones paramétricas son:

Agnesi no presenta ecuaciones paramétricas, pese a que el tratamiento hubiera sido más sencillo, a través de  y 

Teano, pionera de la ciencia matemática

Nos remontamos al siglo VI a.C., época en la que la cultura griega gozaba de un gran esplendor. Es una importante etapa histórica en el campo de las matemáticas y un claro ejemplo de ello lo encontramos en la figura de una de las mujeres más importantes de entonces: TEANO.

Teano nació en Crotone, en Grecia, y para sorpresa de muchos fue esposa de nuestro querido y conocido amigo Pitágoras. Por ello cabe esperar que Teano fuera una de sus más fieles discípulas y que perteneciera a la Escuela Pitagórica de la que más tarde fue maestra.

Teano está considerada como la primera mujer matemática (de ahí que sea la primera que aparece en este blog) y además se tiene constancia de su gran labor científica. Escribió numerosos tratados de Matemáticas, Física y Medicina, y también fue precursora de la investigación. Algunos de sus escritos más relevantes son:
Vida de Pitágoras
Cosmología
Teorema de la proporción aurea
Teoría de números
Construcción del universo
Sobre la virtud

Pero lo más interesante de esta matemática es, sin duda, lo que se conoce como el número de oro, también llamado proporción áurea o razón áurea. Su explicación es sencilla:

El símbolo pitagórico era el pentagrama: la estrella de cinco puntas que se forma uniendo los vértices de un pentágono regular dejando uno en medio.



Pues bien, si dividimos la longitud de la diagonal entre la longitud del lado sale siempre el mismo número. Este número es conocido como la razón áurea, la divina proporción o el número de oro.



Este número se representa con la letra griega
(phi) parece que en homenaje al escultor Fidias que la utilizó para la proporción de sus estatuas.